移动平均线取中
从统计学角度来看,更准确的做法是把移动平均线“取中”(见图9.8a和b)。就是说把每个移动平均值都画在它所覆盖的时间区间的中点上。比如说,与通常的做法相比,10天移动平均线就要向前移5天。20天的移动平均线则应向前移10天。不过,移动平均线取中有个重要缺陷,就是由之产生的趋势改变的信号实在过于滞后。因此,通常,我们还是把移动平均值放在它所筱盖的时间区间内的最后一天,而不是中点。取中技术一般只用在周期分析中,以分离各种潜伏的市场周期。在第十四章我们讨论趋势分解的时候,对取中的移动平均线会有更多的介绍。
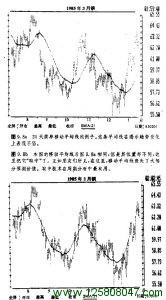
移动平均线与周期现象关系密切
许多市场分析者相信,在市场运动中,时间周期起着重要作用.因为时间周期具有重复再现的特点,并且可以定量测算,所以,我们有可能预测市场出现顶或底的大致时间。从为时6天的短期周期开始,一直到长达54年的康德拉蒂耶夫周期,许多种时间周期同时并存。这是个迷人的技术分析领域,后面专门有一章对此详加阐述。
我们在这里引入周期概念,只是为了说明以下一点:影响某市场的主流周期与这个市场上最恰当的移动平均线之间,似乎颇有关联。换句话说,我们应按照每个市场的主流周期,来相应地调整移动平均线的天数。
看来,移动平均线和周期确实有一定的关系。举例来说,在所有的商品市场上,月周期都是最广为人知的。每个周期都倾向于按照一二个倍数因子,与其上一级长周期,或者下一级短周期和谐地相互呼应。这就是说,上一级长周期是本周期长度的双倍,下一级短周期则是本周期长度的一半。
于是,我们从月周期上或许就能解释5天,10天、20天和40天移动平均线之所以流行的缘故。月周期的长度是20天。40天移动平均值是20天的两倍。10天移动平均值是20天的一半,5天移动平均值又是10天的一半。
在较为通用的移动平均线中(包括4天、9天和18天移动平均值,它们分别是从5天、10天、和20天中导出的),有不少可以用周期的影响以及各级周期之间的和谐关系加以解释。碰巧的是,四周周期也有助于解释四周规则成功之所在。本章稍后就要讲四周规则,以及它的“小兄弟”——二周规则。
菲波纳奇数字在移动平均线法中的应用
在关于艾略特波浪理论的一章中,我们将介绍菲波纳奇数列。不过,在这里我们先要指出,这个神奇的数列—例如13,21,34,55,等等——在移动平均线法中看来也颇有用武之地。这一点不但对于日线图成立,而且在周线图中也适用。在日线图中我们曾提到21天移动平均线,这也是个菲波纳奇数字。在周线图上,不管是在股票市场,还是在商品市场,均证明13周移动平均线很有价值。关于这些数字的深入探讨,我们留给十三章(见图9. 9a到d)。
移动平均线适用于任何时间尺度
移动平均线方法最主要应用于日线图。不过,其实它既可以应用在更长期的趋势分析上,也可以应用于更短期的研究中。我们不应该忽视这两个方面。在股市分析中,长期的移动平均线,例如10周或13周平均线,与30周平均线的组合使用方法,可以说由来已久了,但在商品期货市场上,它们还未受到应有的重视。在连续周线图上,我们可以用10周与30周移动平均线的组合来追踪开始于数年之前的主要趋势(见图9.10)。
从时间尺度上说,如果我们再往另一个方向看看,那么,也可以把移动平均线法应用于日内图上,辅助我们进行短线交易。无疑,在这些短线图表上,移动平均线给出的信号也是有效的。但是,对于当日交易者来说,应对及时是极为关健的,而移动平均线方法天生具有时间滞后的特点,那么,其时间滞后性质是否会损害它在当日交易中的效用呢了这是我给朋友们提出的疑问。
 峰汇在线
峰汇在线




