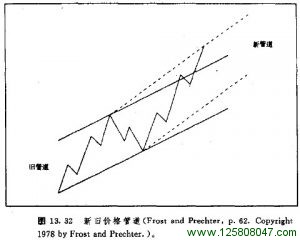
双三浪结构和三三浪结构
调整浪的最后一种类型是两个或三个简单形态的组合,属于较不常见的复杂形态。图珍13.29和13.30是两个例子。在图13.29中,两组a—b—c形态合并起来,形成了七浪。在图13.30中,三组a—b—c。形态合并在一起,形成了十一浪。朋友们请注意,这些形态与经典的交易区间(或者巩固形态)何其相似乃尔。
现在,我们已经介绍了艾略特波浪理论的各种基本的波浪形态。下面我们概要地说一说几个综合性的要领—交替规则和管道技术。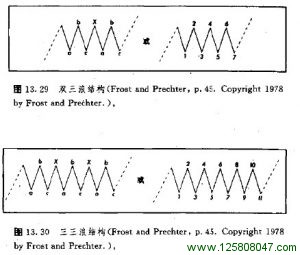
交替规则
从较为广义的角度来看,交替规则(或原理)认为,市场通常不会接连地以同样的方式演变。如果上一次的顶部或底部是这个样子,那么下一回很可能就是另一个样子了。交替规则并不能确切地说明下面出场的是什么,但它可以说明什么可能是不会出现的。就其更具体的应用来看,在绝大部分情况下,它告诉我们应该预期什么类型的调整形态。调整形态交替出现。换个说法,如果调整浪2浪是简单的a—b—c结构,那么4浪很可能就是复杂的形态,比如三角形。反过来,如果2浪是复杂的,那么4浪可能就是简单的。在图13.311中有几个例子。
价格管道
波浪理论还有一个重要的方面,是关于价格管道用法的。在第四章,我们讲过趋势的管道特点。在艾略特这里,价格管道也是侧算价格目标的一个法子,并且也有助于验证波浪序列的完成。一旦上升趁势确立了,我们就可以通过1浪和2浪的底点连接出墓本的上升趋势线.然后,如图13.32所示,我们通过1浪的高点,引出其平行线,这便是管道线。上升趋势常常完全局限于这两条边界线之间。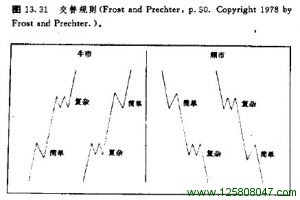
如果3浪开始加速,突破了上方的管道线,那么我们就必须分别从1浪的顶点和2浪的底点出,引出另一组平行线,如图13.32中的虚线所示。最后所得的管道如图13.33所示,下边线沿着二个调整浪——2浪和——4浪——的底点,上边线通常经过3浪的顶点。如果3浪极度强劲,或者是延长浪,那么,上边线或许就得从1浪的顶点引出了。第5浪在终结之前,应当向上抵近上侧的管道线。如果朋友们需要对长期趋势作出管道线,那么建议大家也采用半对数刻度图数,以同算术刻度的图表相参照。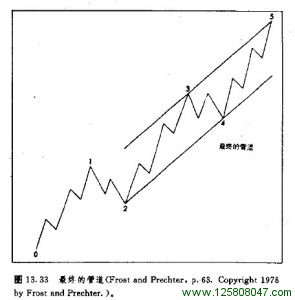
4浪作为支撑区
关于波浪的形态及其要领就快介绍完了,不过下面这个要点我们还需要补充一下,那便是4浪在之后的熊市中所起到的显著的支撑作用。当五浪结构的上升阶段完成后,熊市就出台了。通常,这一轮熊市不会跌过比它低一层次的、前面的第4浪(即在之前的牛市中形成的第4浪)。这是个惯例,虽然也有例外,但是通常看来,第4浪的底还是兜得住这个熊市的。在我们侧算价格下跌的最远目标时,这点信息的确非常有用。
菲波纳奇数列是波浪理论的基础
到过意大利比萨城的人,绝大多数都见过那座著名的斜塔。对于她的建筑师波那纳来说,塔虽然斜了点儿,却不失为一块好纪念碑。波那纳、比萨斜塔和股市、艾略特理论挨得上吗?有点牛头不对马嘴。但是,许多人都不知道,离塔不远,就树立着一个小塑像,他就是13世纪的数学家—里昂纳多·菲波纳奇。那么,菲波纳奇同研究股市行为的艾略特波浪理论又有什么牵连呢?千丝万缕!艾略特在他的《自然法则》中交代,波浪理论的数学基础,就是菲波纳奇在13世纪发现的(更准确地说,是重新发现)一组数列。该数列后来以其发现者命名,一般称为菲波纳奇数列(或菲波纳奇数字)。
菲波纳奇发表了三部主要著作,其中最著名的是《计算的书》。这本书把阿拉伯数字引入欧洲,使之逐步取代了古老的罗马数字。他的著作对后来的数学、物理学、天文学、工程学的发展也作出了贡献。在《计算的书》中,菲波纳奇数列第一次出现,是作为兔子繁殖的数学间题的解答写出来的。这组数列是1,1,2,3,5,8,13,21,34,55,89,144,等等,以至无穷。
这个数列有许多有趣的性质,并不只是在它的数字之间存在连续性关系这一点。
1.任意两个相邻的数字之和,等于两者之后的那个数字。例如,3和5之和为8,5和8之和为13,往下依此类推。
2.除了开始的四个数字外,任意一个数字与相邻的后一个数字之比,均趋向于0.618。例如,1/l=1.00,1/2=0.50,2/3=0.67,3/5=0.60, 5/8=0.625,8/12=0.615,13/21=0.619,往下依此类推。注意,上述比值围绕着0.618上下波动,越往后,波动幅度越小。另外,还请注意1.00,0.50,0.67这几个数值。等后面谈到比例分析、 百分比回撤时。我们再来仔细分说。
3.任意一个数字与相邻的前一个数字的比值约等于1.618,或者说是 1.618的倒数。例如,13/18=1.625,21/13=1.615,34/21=0.619。数字越大,则相应的两种比数越分别接近0.618和1.618。
4.隔一个数字相邻的两个数字的比值趋向于2.618,或者其倒数,0.382。例如.,13/34=0.382,34/21=2.615。
还有其它许多有趣的关系,上述几条是最著名的、最重要的。前面我们说过,菲波纳奇只是重新发现了这个数列。这是因为古希腊和埃及的数学家们早已通晓1.618和0.618这两个比值了。它们就是黄金分割律,或称黄金比数。在音乐、艺术、建筑和生物学中,都有它们的影子。希腊人利用黄金分割律建造了巴特农神殿,埃及人借助黄金比数筑起了大金字塔,毕达哥拉斯、柏拉图、里昂纳多,达·芬奇也都通晓它的性质。
有些研究者对菲波纳奇比数的探究几近走火入魔。有人居然统计了65名妇人的肚脐的高度,宣称其平均值是她们身高的0.618(我们无从知道,他是照肚脐的上边还是下边算起的,当然,更不明白为什么在人身上会出现这个比数)。我们这里的全部目的,是想表明菲波纳奇比值的确在大自然中俯拾皆是,并且实质上也浸透了人类活动。
 峰汇在线
峰汇在线