稳健夏普比率就是RAR除以年度化的月度回报标准差。这个指标对数据变化的敏感度较低,原因与RAR的敏感度低于CAGR的原因相同,上面已经说过。如表12-1所示,稳健指标对测试起止日的变化远不如普通指标敏感。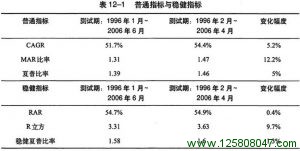
很明显,稳健指标的敏感度要低于现有的指标。R立方指标虽然对首尾两个大衰落的去除也很敏感,但敏感度要低于MAR比率。单次衰落的影响被R立方指标的平均化处理缓和了。所有的稳健指标受数据变化的影响都要小于相应的普通指标。假如新的测试没有改变最大衰落,R立方将与RAR一样只有0.4%的变化,而且与普通指标的差距将更富戏剧性,因为MAR的变动幅度将达到5.2%(等于它的分子CAGR的变化幅度),远远大于RAR的0.4%。
我们从第七章的6种基本交易系统的业绩对比中也能看出稳健指标的优越性。请回忆一下,当我们添加了2006年7~11月这5个月的数据后,所有6种系统的表现都显著下降。但从表12-2和表12-3中可以看出,在这最后几个月的相对不利条件下,稳健指标的状况要比普通指标好得多。表12-2对比了这些系统的RAR和CAGR变化情况。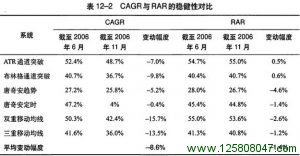
在这段时间内,RAR的变动幅度不到CAGR的1/6。这表明RAR指标比CAGR要稳健得多,也就是说,它在实际交易过程中会表现得更加稳定。R立方与MAR比起来同样如此。表12-3对比了这些系统的R立方和MAR变动幅度。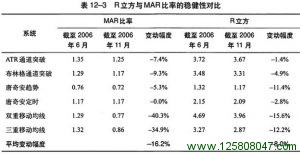
R立方在这段时间内的变动幅度大约是MAR比率的1/2。
相比不稳健指标,稳健指标也不太容易受到运气因素的影响。比如,如果一个交易者因为恰好外出休假而幸运地避开了一次大衰落,他的MAR比率可能比同行们高一些,但这种运气因素会在R立方上暴露出来,因为单单一次事件对R立方的影响并没有这么大。如果你用的是不稳健指标,那么你所得到的理想结果更有可能是好运所致,而不是可以利用的重复性市场行为模式。这也是使用稳健指标的另一个原因。
使用稳健指标还能帮助你避开过度拟合的危害,因为它们不太容易因为数据的微小变动而发生大的变化。请回忆一下,我们在讨论过度拟合现象的时候曾经拿双重移动均线系统做了个试验,添加了几条法则以提高它的表现。意在降低衰落程度的新法则令系统的CAGR从41.4%上升到了45.7%(涨幅10.3%),MAR比率从0.74上升到1.17(涨幅60%)。相比之下,稳健的回报率指标RAR仅从53.5%上升到53.75%,涨幅不过0.4%;稳健的风险回报比指标R立方从3.29上升到3.86,仅提高17.3%。可见,稳健指标不太容易因为少数交易的调整而呈现大的改进。因此,由于曲线拟合手段往往只是对少数交易有益,如果你使用稳健指标,你就不太容易用曲线拟合的手段来显著改善系统的表现。
下面让我们考虑一下其他几个对历史检验的预测价值有影响的因素。
 峰汇在线
峰汇在线




